三角ロジックで基本形を確認する

 2002.8.25

三角ロジックは論理的思考の基礎となる考え方です。演繹や帰納という考え方も、三角ロジックをベースに考えられます。より論理的な思考をするためには、この三角ロジックを階層的に適用していきます。

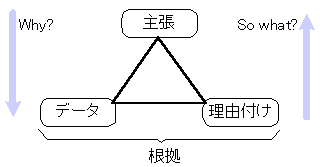
三角ロジックとは

論理的な主張には、客観的なデータと、そのデータと主張を結びつける理由付けが必要です。主張、データ、理由付けによる論理を三角ロジックと呼びます。主張に対する「Why?」という疑問の答えが、データと理由付け（合わせて根拠）で示されます。逆に根拠に対する「So what?」という疑問の答えが主張になります。

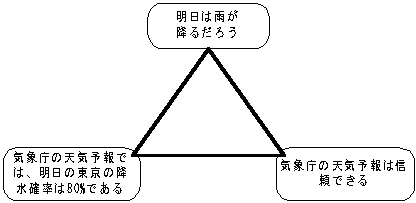
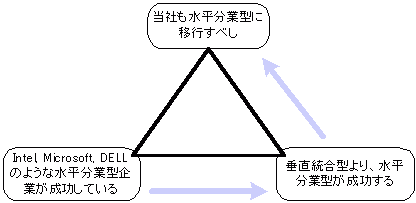
三角ロジックの具体例

帰納と演繹

演繹

理由付けを認めたなら、主張も必ず認めなければならないような導出です。一般からの個別事象の導出とも言えます。理由付けを主張の拠り所としています。

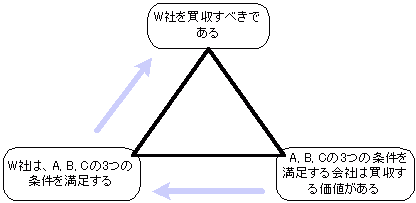
帰納

個別の事例からの一般論の導出です。データを主張の拠り所としています。

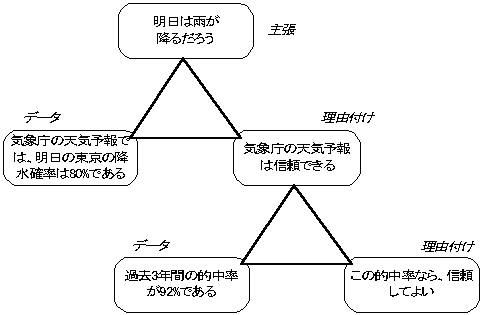
階層三角ロジック

理由付けは一種の主張と考えられます。理由付けを主張とすれば、そこにまたデ-タと理由付けが必要になります。これを階層的に繰り返していけば、より強固な論理となります。

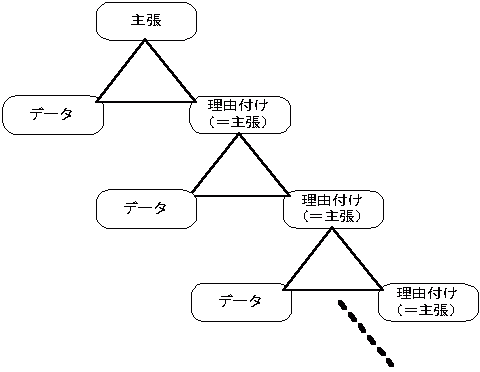
階層的三角ロジックの具体例